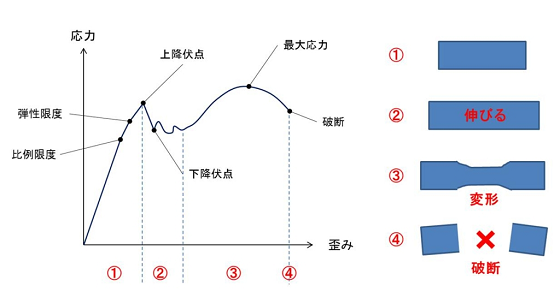
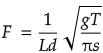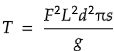音程の保持力（狂いにくさ）を得るテクニックは人様々である。よく言われるのが　絞る　或いは　押し込む　やり方だ。

一般的にこの方法は、一旦要求より高い音程に上げることで高い張力を獲得し、音程まで下げるときにピンを前傾させながら強め゙に打鍵して下げていく。こうして、ピンそのものの捻れや、そのsc1.0側のピンブッシュやピン板を圧迫して得られる一種のバネによる引っ張りに対する抵抗で音程を保持する。もしsp1に高めの張力が残っていれば、それも抵抗となる。

bp1〜bp5の各ポイントも保持力の向上に与っている。また、はずしてみれば明らかだが、弦のそれら屈曲ポイントに対応した位置には屈曲ができていて、いわば引っかかりになるので、これも保持力の向上に役立っているだろう。

これらのことを仮定して、今張力を高くする場合の実際の操作と、tpに近いsc1.0、sc1.1、そして発音される音程に直接かかわるsl各弦長の、操作に伴う動きを考えてみよう。

張力を高くするのだから、チューニングピンの動きはcwだ。そうすると

1. sc1.0の張力が高まる
2. bp1にあたる弦が動く
3. sc1.1の張力が高まる

という変化が順番に起こるのではないだろうか。そしてsc1の張力Tは

• t を 2が起こる直前のsc1.0の張力

とすると、底辺の長さと底辺と斜辺のなす角度から斜辺を求めるので

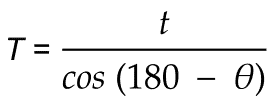
となる。したがって動静のしきい値は

• g を重力加速度
• μ を弦の静止摩擦係数

とおいて、斜辺と角度から高さを求めるので

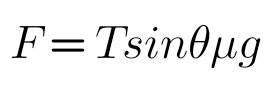
そして、この張力が次の屈曲点であるbp2にあたる弦を動かす十分な大きさであるとき、次に

4. bp2に当たる弦が動く
5. slの張力が高まる

変化が起きて、聴覚で「音程が高くなった」と判定される。

設計のとき、計算上はsl ⇔ sc3.0 のY方向の角度は考慮されないのではないか。これが先の投稿の結論である。ここからは、この仮定上で考えることにしたい。

ところで、張力計算の目的の１つは、各slに発音に適した張力を与えることだろう。線密度が同じ（弦の比重と太さが同じ）で長さも同じなら、周波数が高い方が振動のエネルギーは増える＝音量がふえるから、では切れる寸前がよいのか？ピアノ線の応力応答は下図¹の通りだ。

聞きかじりだが、張力は破断限界の70%程度がよいと言われているそうだ。が、実際の調律作業では一旦上げ越すことが多いし、ハンマーが衝突して外力が加わったときに生じる定常波の周波数、つまりピッチを変更できなければならないので、張力の増減に対し歪みの可塑性が保証されている比例限度を超えることはないだろうから、比例限度の70%程度ということだろうか。

どのポイントを基準に70%なのかはさておき、上の図をからは、先の投稿で触れた弦圧をもちださなくても、作業の都合や調律の保ち（保持力）のために上げ越しの幅を大きくとるのは、かなり危険なことだというのが見て取れる。

1. 図　あろろい ↩︎

ピアノの弦は、なかだかい造りの響板に張られることでY方向に屈曲が生じ、その方向の分力によって響板を圧縮している。音響学では、そうして圧縮することで響板材に本来的に内在する鳴り難さを低減し、弦振動に共鳴させて発音させている、と考えられている。この理論に基づけば、調律は響板に適切な圧力をかける作業である。そして、設計の側からみた調律の目的は、求める音程毎に設計弦長に応じて張力を補正する作業ということになる。

張力の計算式¹を見よう。

ここで変数は

• F = 周波数 (Hz)
• L = 弦長 (cm)
• d = 弦の直径 (cm)
• T = 張力(g)

そして２つの定数

• g = 重力加速度 (cm/sec²)
• s = 弦の比重 (g/cm³)

周波数を求める式

（π は円周率）から張力を求める式

が導かれる。

２点間を引っ張ったときのことを述べているのだから当然だが、この式には角度に対応する変数は現れない。Y方向の分力、我々が謂うところの弦圧は、理論上は響板を圧縮するために必須なのに、計算では考慮されない訳だ。

響板のクラウンは、比較的全体張力が低いとされているスタインウェイでも、中央付近で9〜11mmに及ぶと、ハンブルク工場で聞いた覚えがある。オーダー10mm公差 ±1mmなのかもしれない。もっと差が大きかった気もするのだが、いずれにせよ最終的な弦が響板に与える力は250Kg〜300Kg近くにのぼり、10mmを超える厚みがあり響棒で弓なりのフォルムを補強されたスプルースの板を押し下げる。

設計計算上は、弦各部の張力をそれぞれ計算して足し合わせるのだろうか。

それとも、設計では、Y方向の分力は計算上無視するということなら、設計が指しているのが製品の理想的な状態である以上、現物では駒を挟んだ弦のY方向の屈曲は無視できるほど小さい、つまり　弦圧 ≒ ０　ということになりはしないか。

1. 出典　http://park11.wakwak.com/~md440/temp/mwcalc.html ↩︎